诈唬是扑克游戏中的重要组成部分，每一个优秀的玩家都应该牢记它。从不诈唬或者太频繁地诈唬，对一个扑克玩家来说都是巨大的错误。如何找到适当的平衡点？什么时候诈唬才是理想的选择？什么时候，以什么样的频率对某些玩家诈唬才能打出有收益的扑克呢？

 

这篇文章会涉及到诈唬的数学背景，并利用博弈论阐述一些可能的策略。

这篇文章的主要内容

      • 数学背景

      • 最佳策略

      • 纳什均衡点

前面两点我们在前几天的文章中已经讨论过...今天，我们要说的是第三点：

一些特殊情况中的预期回报

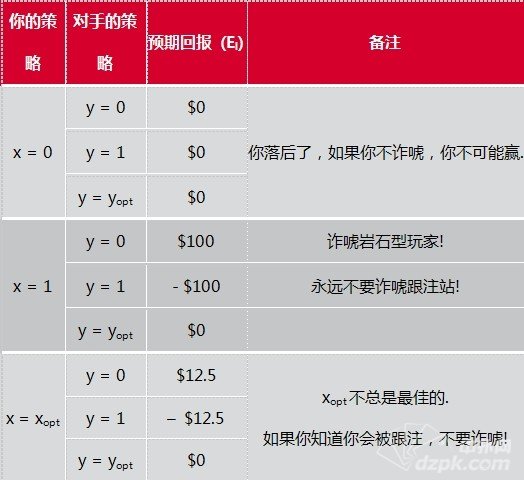
下面是两张展示特殊情况中的预期回报的图表。第一张图表显示当你的听型牌失败时的预期回报，用给定的例子计算：

你的对手的预期回报是你的预期回报的负数，加上已经在底池中的$100。(他会得到你在下注轮的净损失，加上 现有的底池。当然如果你赢下底池的话，你的净损失是– $100，而他不会得到任何东西。来看看最简单的情况：当你的预期回报是0时，你的筹码量不会发生变化。因此你不会赢下底池，赢得底池的是你的对手。因为 我们已经玩到了河牌圈，所以这不是一个零和博弈。)

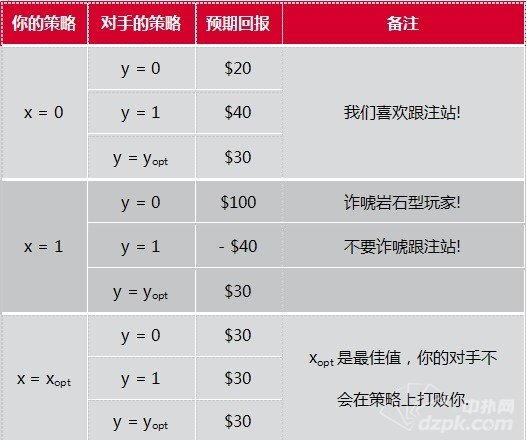
当你知道什么时候诈唬，什么时候价值下注，而对手却不知道时，对他来说(也可能对你)，下面的这个图表 会更有用。这张表显示的是，综合你的获胜牌和失败牌之后的你的预期回报。在类似的情况中，你有20%的时候会领先，80%的时候会落后。因此你的平均预期 回报是 qEw + (1 – q)El. (这个结果的负值加上底池现有的$100是你的对手的预期回报Eop。)

结论

当你面对一个优秀的对手时，最好的选择就是利用纳什均衡点为你提供的策略：xopt。在这种情况你的对手会用 yopt的策略打牌。如果他没有，他就犯了错误(也说明他不是一个优秀的玩家)，你可以利用他的错误找到最佳的打法。如果他经常跟注，就少诈唬他，如果他 很少跟注，就多诈唬他。如果你能猜测他的跟注频率，就可以根据预期回报最大化的原则，计算自己应该诈唬的频率。

附录

计算yopt的值

如果y = yopt，你的预期回报不会改变，无论x是多少。让我们先让x = 0，这时你什么牌也赢不了，公式是：

El, x=0 = 0. 

现在让x = 1. El的公式变为

El, x=1 = (1 – yopt)P – yoptB.

因为x=0和x=1时的预期回报是一样的，所以

(1 – yopt)P – yoptB = 0,

所以

    (1 – yopt)P = yoptB,

    P – yoptP = yoptB,

    P = yopt(P + B), 

最后

yopt = P/(P + B).

从对手的角度来看

现在让我们以对手的视角看看这个问题。首先我们要列出他的预期回报Eop。因为他不知道你是领先还是落后，所以他的预期回报还受q的影响，因此公式有一点复杂：

Eop = – qyB + q(1 – y)0 + (1 – q)[xy(P + B) + x(1 – y)0 + (1 – x)P]. 

第一项表示你有能取胜的牌，你下注，他跟注，并损失了这个跟注。第二项表示你持有能获胜的一手牌，但是他弃 牌，没有赢到或损失任何东西。剩下的部分表示他领先时的情况。方括号中的第一部分表示你诈唬，他跟注，他赢得底池和你的下注的情况。中间部分表示当你诈 唬，他弃牌时的情况，没有盈利和损失，最后一部分表示当你弃牌时，他赢得底池的情况(可能是他在你之后过牌，赢得摊牌，也可能是他下注，迫使你弃牌).

省略其中为0的部分，我们得到

Eop = (1 – q)[xy(P + B) + (1 – x)P] – qyB.

如果你的对手知道你从不诈唬(x = 0)，那他的最佳打法是什么？他永远不会跟注，在上面的公式中如果用0代替x，我们得到

Eop x=0 = (1 – q)P– qyB. 

为了使结果最大化，我们必须让y = 0 (永远不跟注)。

另一方面，如果你的对手知道你总是诈唬(x = 1)，那他最好的回应就不那么明显了。如果x = 1，我们得到

Eop x=1 = (1 – q)y(P + B) – qyB = y[(1 – q)(P + B) – qB].

如果

(1 – q)(P + B) – qB > 0,

y = 1 (总是跟注)会最大化对手的预期回报。

如果

(1 – q)(P + B) – qB < 0,

他就应该使用 y = 0 (永远不跟注)的策略。

(1 – q)(P + B) – qB < 0

意味着

    (1 – q)(P + B) < qB,

    P + B – qP – qB < qB,

    P + B < q(P + 2B), 

最后

q > (P + B)/(P + 2B).

在我们的例子中，P = B = $100，如果q > 2/3，你的对手应该永不跟注(即使他知道你总是下注;因此在这种情况中你总是应该诈唬)， 当q < 2/3时，他应该总是跟注(如果他知道你总是诈唬)。记住，这个q的值也仅取决于底池大小和下注大小。

计算xopt的值

如果x = xopt，你的对手的预期回报不会改变，无论y是多少。和之前一样，先让y = 0。Eop的公式为

Eop y=0 = (1 – q)(1 – xopt)P.

现在让y = 1。我们得到

Eop y=1 = (1 – q)[ xopt (P + B) + (1 – xopt)P] – qB.

因为y=0和y=1时的Eop是一样，我们得到

(1 – q)(1 – xopt)P = (1 – q)[ xopt (P + B) + (1 – xopt)P] – qB,

因此

qB = (1 – q) xopt (P + B)

(两边都有(1 – q)(1 – xopt)P，因此可以消掉)，所以最终我们得到

xopt = qB/[(1 – q)(P + B)].

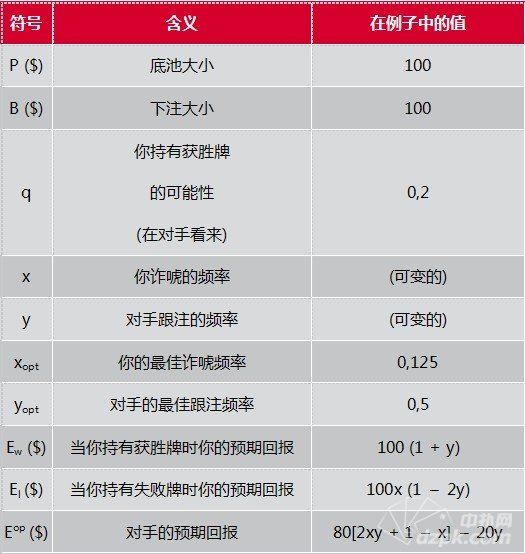
当我们讨论可能性时，我们通常用 0.2代替20%，用0.5代替50%等等。一件不可能的事件发生的可能性是0 (0%)，一件确定的事发生的可能性是1 (100%)。剩下的其他事件发生的可能性在0和1之间。