虽然很多玩家都知道什么是诈唬和英雄跟注，但他们却没真正理解为什么要使用它们，或如何用它们盈利。

所以这篇文章我们将对诈唬和英雄跟注背后的数学原理与依据进行探讨。

希望能帮助大家理解自己的诈唬和英雄跟注需要达到多高的成功率才能实现长期获利。

☆ 什么是英雄跟注？ ☆

诈唬（偷鸡）是什么大家都知道，这里就不再多做解释了。

然而，并不是每个人都知道什么是英雄跟注，所以我们先来快速定义一下它。

“英雄跟注”就是指你用一手边缘牌在河牌圈跟注对手的潜在诈唬，并希望能成功抓诈（抓鸡）。

之所以被称为“英雄跟注”，是因为你抓鸡成功的样子就像个伟岸的英雄，全桌人都对你牛B的读牌能力感到钦佩！

例如，你用8♣8♥跟注了一名激进对手的翻牌前加注。翻牌发出2♦ 4♦ 9♣，对手持续下注，你跟注。转牌发出10♠，对手再次下注，你跟注。河牌发出7♣，对手直接全下，你思考了几分钟，最终决定跟注。结果对手无奈亮出A♦K♦，你成功拿下这个超大底池。这里河牌圈的跟注就可以被视为一次英雄跟注，因为你用一手边缘牌（只是第三顺位的一个对子）成功抓到了对手的诈唬。

☆ 它们不需要每次都成功 ☆

关于诈唬和英雄跟注，你最先需要了解的就是，它们实现赢利并不需要100%的成功率；你也不应该期望它们能一直成功。很多新手玩家都在为这一简单的事实而苦苦挣扎，且过于情绪化地陷入自己的诈唬和英雄跟注中。当诈唬或英雄跟注失败时，他们就会沮丧不安，这显然是错误的。他们根本不了解诈唬和英雄跟注背后的基本数学原理，只是一味地让自己上头失控，在牌桌上无能狂怒。

与其一味沮丧不安，不如深入了解诈唬和英雄跟注背后的数学。要知道，诈唬和英雄跟注通常只需要一丢丢成功率就可以实现赢利。我们会在接下来的内容中对这一点进行探讨。当它们成功时，我们当然应该高兴，可如果它们没能成功，我们也无需纠结，只需要耸耸肩将注意力转向下一手牌。

☆ 诈唬的成功率需要达到多少？ ☆

当我们在诈唬时，其实就是冒着所投入下注量的风险去赢底池里已经有的钱。因此，我们就会有一个简单的风险回报比，即冒一定金额的风险，去赢一定金额的钱：

●风险：我方下注量

●回报：底池

简单示例

底池里有100刀，我们诈唬下注50刀。

我们的诈唬需要达到多少的成功率才能实现赢利？

●风险回报比（回报:风险）= $100 : $50 = 2:1 = 1/3 = 33.3%

在这种情况下，我们是冒着50刀的风险去赢底池中已有的100刀。从上面的比率可以看出，我们的保本点是33.3%。所以，我们的诈唬只需要达到33.3%的成功率就可以实现赢亏平衡。因此，只要它的成功率超过33.3%，就是有利可图的！

☆ 诈唬赢亏平衡表 ☆

下表列出了基于下注量，我们的诈唬成功率需要达到多少才能实现赢亏平衡。从该表中可以看出，如果我们只下注1/3底池作为诈唬，那么它的成功率只需达到25%就能实现赢亏平衡。

也就是说，如果它在1/4以上的时间里都能奏效，那它就是有利可图的。

☆ 诈唬提醒 ☆

数学上就这么简单，但还有更多其他因素会影响诈唬的成功率，比如牌面结构、对手眼中我们的范围、有效筹码量深度、对手的打法风格、游戏级别等等，不过这些已经超出文章的讨论范畴。

要判断一次诈唬是否能成功，你需要将各种信息都纳入考虑。你要明白，这里所讨论的简单数学原理并不能直接告诉我们某次诈唬在某个特定场景下能否成功，只能明确这次诈唬需要达到多高的成功率才算有利可图，具体取决于你的诈唬下注量。学习何时以及如何成功诈唬，是你在扑克游戏中需要掌握的一项完全不同的组合技能。

☆ 英雄跟注的成功率需要达到多少？ ☆

诈唬讨论完了，我们再来谈谈英雄跟注。英雄跟注，以及它需要达到多高的成功率，完全取决于我们所获得的底池赔率。如果对手提供了25%的底池赔率，那么我们的英雄跟注的成功率就需要超过25%才算有利可图。

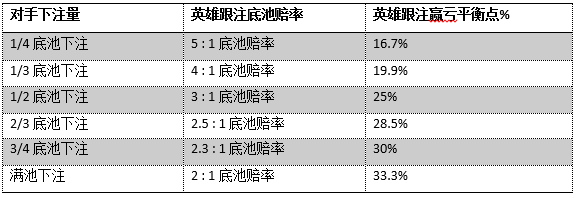
需要注意的是，就像诈唬一样，英雄跟注也不需要多高的成功率，这一点可以从下面这张英雄跟注赢亏平衡表中看出一二。

英雄跟注赢亏平衡表

☆ 英雄跟注提醒 ☆

就像诈唬一样，想要做出有利可图的英雄跟注也需要很多因素。我们确实需要了解对手的打法风格，以确定他在河牌圈是否是在诈唬。

学习对对手范围进行读牌并了解其与牌面结构的联系，以及了解对手在河牌圈诈唬的倾向和喜好，再加上之前提到过的诸多其他因素，都将有助于提高你英雄跟注的整体成功率。

要提醒大家的是，文章所讨论的数学原理不会告诉你某次英雄跟注能否成功，只能让你明确它需要达到多高的成功率才算有利可图。

☆ 结论 ☆

诈唬和英雄跟注需要多高的成功率才算有利可图，该概念背后的数学原理其实非常简单。只可惜，很多人都忽略了在游戏中去使用它们，尤其是当涉及到诈唬时。诈唬和英雄跟注的伟大之处就在于，它们根本不需要多高的成功率就能实现长期赢利。

请牢记，了解它们不需要多高的成功率并不代表你就可以随时随地乱偷一通或胡乱跟注。无论何时当你想要做出诈唬或英雄跟注的决策时，除了其背后的数学原理，也一定要将其他各种因素都纳入考虑。